Pembahasan Bebras Card 7+

Berikut ini, soal soal bebras Card 7+ dan pembahasannya.

Beri si Berang-Berang kecil mempunyai stempel

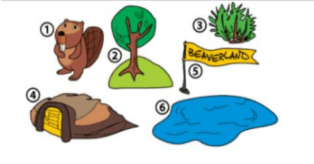
Dia membuat kreasi ini:

Untuk membuat kreasi itu, beri harus menempel stempel dengan urutan : …

Pembahasan

Karena 6 berada pada lapisan paling bawah, selanjutnya diikuti 4 diatas stempel 6, 5 ditempel diatas 4, lalu ditempel 3 diatas 5, dan terakhir 1 diatas 3, maka jawaban nya 6-2-5-4-3-1

---

Ada beberapa ekor kepik dalam grid yang terdiri dari 16 sel. Sebuah sel dikatakan bertetangga dengan sel lainnya jika sisi atau sudut/pojok keduanya bersebelahan, ini berarti setiap sel dapat mempunyai sampai 8 tetangga.

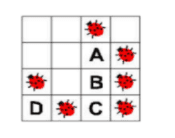
Pada gambar di atas, sel manakah yang dikelilingi oleh paling banyak kepik? Pilih salah satu!

Pembahasan

Karena memiliki 4 tetangga kepik, maka jawaban nya B

---

Beri si Berang-Berang dari Perancis sedang senang memakai kaos yang ada logo gambar dirinya. Dia ingin memakai warna yang berbeda-beda, berganti setiap hari, seperti warna pada bendera Perancis. Hari ini dia memakai kaos warna biru, besok akan memakai warna putih, dan lusa akan memakai warna merah. Pada hari ke-sepuluh, dia akan memakai warna apa?

Pembahasan

Hari ke :  

1. Biru
2. Putih
3. Merah
4. Biru
5. Putih
6. Merah
7. Biru
8. Putih
9. Merah
10. Biru

Maka, jawaban nya adalah Biru

---

Bebras Joni ingin melakukan perjalanan untuk mengujungi 5 kota di negara: Kotasatu, Kotadua, Kotatiga, Kotaempat, Kotalima, Kotaenam. Kota-kota tersebut dihubungkan dengan jalur bus. Rute bus yang tersedia (dalam dua arah) adalah sebagai berikut: 

• Kotatiga –> Kotasatu
• Kotasatu -> Kotadua
• Kotaenam -> Kotatiga
• Kotalima -> Kotaempat

Jika Joni memulai perjalanannya dari Kotatiga dengan bus, kota mana yang tidak dapat dikunjungi?

Pembahasan

Jika aturan diatas digambarkan, akan menghasilkan 

Maka, jika berangkat dari kota 3 tidak akan bisa datang ke KOTA LIMA.

---

Si berang-berang ingin menjadi ninja dan menentukan namanya. Nama ninja dibuat dengan mengganti setiap huruf yang berasal dari nama sesungguhnya dengan suku-suku kata sesuai dengan table berikut: 

Misalnya “BEBRAS” memiliki nama ninja “pikupishikaari”. Jika nama ninjanya adalah “zukame moru”, siapa namanya yang sesungguhnya?

Pembahasan

Kita akan memisahkan suku kata dari “zukame moru” lalu dicocokan dengan kamus kata ninja.

Zu : J

Ka : A

Me : K

Mo : O

Ru : V

Maka, jawabannya adalah JAKOV

---

Violeta ingin mengirim pesan kepada Leo. Pesan dipecah menjadi potongan maksimal 3 huruf yang ditulis dalam kartu dan diberi nomor urut. Untuk mengerti pesan aslinya, leo harus mengurutkan kartu sesuai nomor kartu. Misalnya untuk mengirim pesan DANCETIME, Violeta membuat 3 kartu sebagai berikut:

Saat Leo menerima urutan kartu berikut: 

Apa pesan aslinya?

Pembahasan

Ketika kita urutkan maka menjadi: GET-HOC-KEY-STI-CKS.

---

Bacalah kata-kata yang bisa ditemukan pada pohon ini: 

Tree, trek, tram, trap, teen, teem, team.

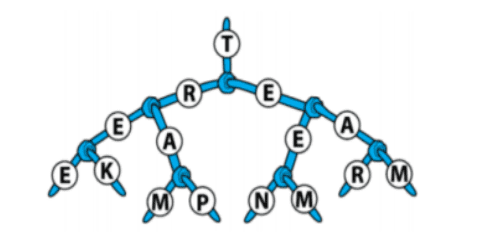
Ternyata ada 1 kata yang ketinggalan. Kata apakah itu?

Pembahasan

Cara membaca pohonnya adalah dengan mengurutkan kata dari atas hingga cabang terbawah. Contohnya saat membaca TREE, dan TREK. Jika ditelusuri semua, maka kata yang ketinggalan adalah TEAR.

---

Alkisah ditemukan beberapa planet baru seperti ini:

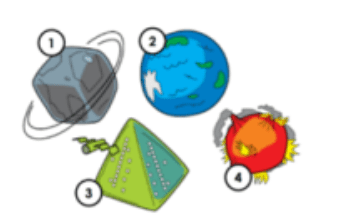
Planet Tersebut dihuni oleh mahluk-mahluk ini:

Cocokkan gambar makhluk tersebut dengan Planet tempat tinggalnya yang sesuai.

Pembahasan

Cara mencocokkannya adalah dengan melihat bentuk kepala penghuni tersebut dengan bentuk dari planetnya. Maka jawaban yang benar adalah 1-B, 2-A, 3-C, 4-D

---

Karu si Kanguru membangun sebuah jemuran baju. Dia ingin memperkuat sebuah tiang di jemuran itu, supaya tidak mudah rusak oleh berang-berang. Akan tetapi, Karu hanya bisa memperkuat 1 tiang saja. Tiang mana yang paling penting untuk diperkuat?

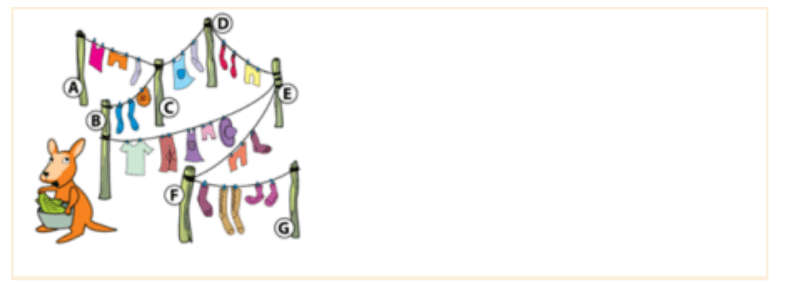
Pembahasan

Pertama kita lihat berapa banyak suatu tiang terhubung dengan tiang lainnya. Maka akan didapatkan bahwa tiang C dan tiang E memiliki hubungan terbanyak, yaitu sebanyak 3 hubungan. Selanjutnya kita akan hitung berapa banyak baju yang digantung pada tiap tiang tersebut. Dari tiang C kita mendapatkan 8 baju, sedangkan tiang E kita mendapatkan 10 baju. Maka tiang yang paling penting untuk diperkuat adalah tiang E. Maka jawaban nya adalah E.

---

Jaka si berang-berang duduk di pinggir jalan menghitung mobil warna-warni yang lewat. Di akhir hari ia mencatat:

• Mobil biru ada 10 
• Mobil merah ada 44
• Mobil putih ada 3
• Mobil hijau ada 8 
• Mobil hitam ada 15

Jaka mengetikkan angka itu memakai program computer dan hasilnya sebuah diagram batang sebagai berikut: 

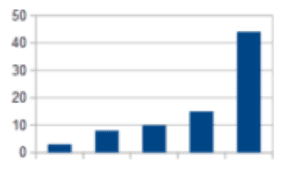
Tetapi sayangnya, diagram tersebut tidak menunjukkan warna mobil, mobil warna apa yang digambarkan pada diagram batang paling tengah?

Pembahasan

Pada soal kita diminta untuk membaca suatu grafik batang. Cara membacanya adalah untuk melihat seberapa tinggi batang tersebut dibandingkan nilai disamping maka itulah besar nilai dari batang tersebut. Sehingga batang ditengah memiliki nilai 10. Maka mobil dengan nilai 10 adalah mobil berwarna biru, maka jawaban nya adalah Biru 

---

Terdapat dua jenis anjing yang berbaris seperti tampak dalam gambar berikut ini

Suatu pertukaran tempat dapat terjadi antara dua anjing yang berdiri bersebelahan. Akan dilakukan beberapa kali pertukaran tempat, sehingga tiga anjing besar akan berdiri dalam tiga posisi yang bersebelahan.

Berapakah banyaknya pertukaran sesedikit mungkin yang diperlukan?

Pembahasan

Caranya adalah kita memindahkan anjing pada urutan pertama DUA kali ke kanan sehingga berada di samping anjing besar kedua. Lalu anjing besar di posisi paling akhir akan kita pindah ke kiri sebanyak EMPAT langkah ke samping anjing besar kedua. Maka total langkah pertukaran yang dibutuhkan adalah 6 kali. Maka jawaban nya adalah 6.

---

Si Bebras dapat memutar roda ke kanan atau ke kiri. Pada setiap sekali putaran, roda berputar, satu Langkah dan panah menunjuk ke warna berikutnya, gambar berikut menunjukkan kondisi awal roda, dan kondisi setelah roda diputar satu kali ke kiri:

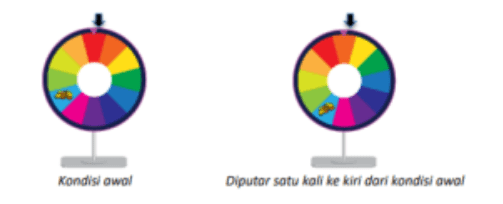
Jika si Bebras ingin menenangkan koin seperti pada kondisi awal (panah menunjukkan warna merah dengan gambar koin seperti pada kondisi awal), beberapa kali putaran roda paling sedikit yang dilakukan pada kondisi awal?

Pembahasan

Kita bisa lihat jika jarak dari warna merah ke hadiah koin adalah 4 warna. Jika satu putaran ke kiri menggerakkan 1 langkah warna maka dibutuhkan empat putaran untuk mendapatkan hadiah koin tersebut, maka jawabannya adalah 4

---

Beri si berang-berang membuat sebuah robot yang dapat bergerak di air sesuai aturan ini: 

1. Bergerak ke depan
2. Jika memungkinkan, belok ke kiri

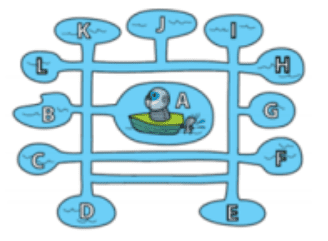
Robot berangkat dari kolam A. di kolam manakah robot akan berhenti?

Pembahasan

Kita mulai dari persimpangan pertama antara kolam A ke B, disini maka robot akan mengambil belok ke kiri hingga sampai ke persimpangan kolam C. disini robot kembali mengambil belok ke kiri. Hal ini terus berulang pada persimpangan kolam F, kolam I dan kolam K. Hingga akhirnya kembali lagi ke persimpangan antara Kolam B dan kolam A. Namun karena kali ini posisi robot datang dari arah yang berbeda, maka robot akan belok ke kiri yaitu ke kolam A. maka robot akan berhenti di Kolam A karena tidak ada jalan yang lain lagi. Maka jawaban nya adalah A

---

Bebras Jordan menebang pohon dan memotongnya sehingga setiap pohon menghasilkan batang pohon yang panjangnya 10 meter.

Bebras Ali ingin membangun bendungan dan membutuhkan kayu sepanjang 4 meter sebanyak 7 batang, dan kayu sepanjang 3 meter sepanjang 7 batang. Ali dapat memotong batang pohon yang sudah dipotong Jordan sesuai dengan keperluannya. Jordan ingin memberikan batang pohon kepada Ali dengan jumlah sesedikit mungkin

Berapa banyak batang pohon minimal yang dapat dipakai Ali untuk membangun kandungan?

Pembahasan

Caranya adalah dengan kita mengurangi panjang dari masing-masing balok kayu tersebut sehingga tidak memungkinkan lagi dipotong untuk mencukupi 3m atau 4m

1. Batang Kayu pertama akan dibuatkan 2 batang 4m (sisa 2m, tidak bisa untuk yang lain)
2. Batang kayu kedua akan dibuatkan 2 batang 4m (sisa 2m, tidak bisa untuk yang lain)
3. Batang kayu ketiga akan dibuatkan 2 batang 4m (sisa 2m, tidak bisa untuk yang lain)
4. Batang kayu keempat akan dibuatkan 1 batang 4m dan 2 batang 3m (tidak ada sisa)
5. Batang kayu kelima akan dibuatkan 3 batang 3m (sisa 1m, tidak bisa untuk yang lain)
6. Batang kayu keenam akan dibuatkan 2 batang 3m

Maka, total batang kayu yang dibutuhkan adalah 6 batang.Maka jawaban nya adalah 6.

---

Bantulah si Robot hijau keluar dari lorong

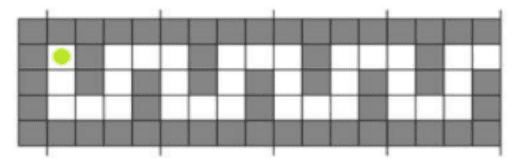
Robot dapat bergerak ke empat arah: Kanan (R), Bawah (B), Kiri (L), atau atas (A).

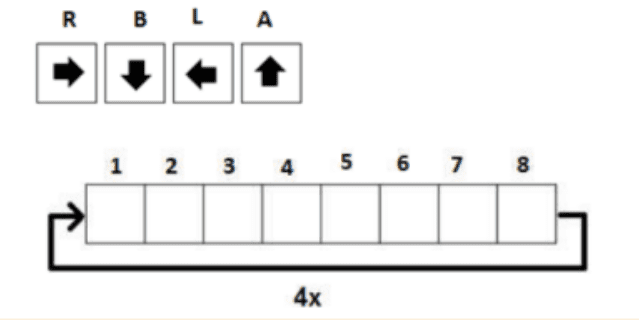
Isilah kotak-kotak tersebut untuk membuat suatu urutan instruksi yang terbentuk harus diulang 4 kali agar robot tersebut dapat dari Lorong.

Pembahasan

BB-RR-AA-RR.

---

Seekor berang-berang sedang mengerjakan set log dengan membandingkan dua log yang berdekatan. Dia membandingkan yang pertama log dengan yang kedua, dan jika sudah habis, dia menukar dua log ini. Kemudian dia membandingkan log kedua dengan yang ketiga, dan seterusnya. Ketika mencoba memasukkan masuk ke tempat yang benar, dia sudah memiliki semua log di sebelah kirinya yang diurutkan, jadi dia menukar log itu dengan log di sebelah kiri sampai posisinya benar. Ini dapat diulang sampai semua log berada diurutkan (misalkan, dari yang terpendek ke yang terpanjang). Berapa banyak pertukaran yang perlu berang-berang tersebut lakukan agar benar?

Pembahasan

Tabel berikut menunjukkan langkah-langkah untuk mengurutkan log {7, 5, 10, 9, 15, 13, 2 , 8, 17, 20}.

Pada setiap langkah, log kunci yang sedang  dipertimbangkan akan digarisbawahi. Log kunci yang dipindahkan (atau dibiarkan di tempatnya karena memerlukan waktu yang panjang untuk dipertimbangkan) pada langkah sebelumnya ditampilkan dalam huruf tebal.

Total 13 pergantian 

Apabila ada kasus yang buruk karena file tersusun di reverse order, maka pergantian angkanya adalah 

1+ 2 + 3 + … + (n-1) = n x (n-1)/2

---

Bubble sort adalah algoritma yang didasarkan pada gagasan untuk membandingkan pasangan elemen yang berdekatan secara berulang dan kemudian menukar posisi mereka jika ada dalam urutan yang salah.

Dalam Bubble Sort, elemen bergerak ke arah yang berbeda dengan kecepatan yang berbeda:

– Elemen yang harus bergerak menuju akhir dapat bergerak cepat karena dapat mengambil bagian dalam pertukaran berturut-turut.

– Elemen yang harus bergerak ke awal daftar tidak dapat bergerak lebih cepat dari satu langkah per lintasan, jadi elemen bergerak ke awal dengan sangat lambat.

Jika elemen terkecil berada di ujung, dibutuhkan (n-1) lintasan untuk memindahkannya ke awal.

Ini telah menyebabkan jenis elemen ini masing-masing dinamai kelinci dan kura-kura (setelah karakter dalam dongeng Aesops The Tortoise and the Hare).  Foto mana yang menggambarkan Bubble Sort?

Pembahasan

D adalah jawaban yang tepat

Kita harus memperhatikan : 

• Elemen yang mendekati akhir dapat bergerak dengan cepat – mereka harus menjadi kelinci (8, 7, 9).
• Elemen yang baru mulai dari awal daftar tidak dapat bergerak dengan cepat, jadi elemen bergerak ke awal dengan sangat lambat – merek harus menjadi kura-kura (1,3,5)

---

Berang-berang berenang dari kota A mengunjungi setiap 3 kota (B, C, D) hanya sekali dan Kembali lagi ke A. Jalur tempuh diestimasikan oleh beb-coins dan angka yang tertulis. Berang-berang ingin mengaplikasikan Nearest-Neighbour Algorithm, yang mana sudah dijelaskan dari judul : 

1. Mulai dari titik A (rumah)
2. Dimanapun anda di dalam perjalanan keliling ke kota tetangga termurah yang belum pernah dikunjungi
3. Tetap ulangi Langkah (b) sampai anda mengunjungi semua kota
4. Dari kota yang paling terakhir kali dikunjungi, langsung pulang ke asal

Ada 3 rute yang memungkinkan : 

• A B D C A = 4 + 2 + 10 + 14 = 30
• A B C D A = 4 + 3 + 10 + 6 = 23
• A C B D A = 14 + 3 + 2 + 6 = 25

Manakah yang diperoleh dengan Nearest Neighbour Algorithm?

Pembahasan

Berang-berang yang mengaplikasikan Nearest Neighbour Algorithm dan memilih rute yang dekat dari A (4), yang berarti dia akan mengunjungi B. dari B, ada 3 jalan: A (rumah berang-berang tersebut), D (2) dan C(3) – dan rute yang paling dekat adalah D. Jadi, rute berang-berang tersebut adalah: A B D C A

---

Sebuah algoritma yang sudah ditambahkan untuk komputasi primer bekerja seperti berikut ini: 

• Bikin sebuah daftar angka dari 2 ke yang terbesar sesuai keinginan anda; panggil angka yang paling maksimal dari nomor n 
• Tambahkan angka pertama dari daftar saat ini ke dalam daftar bilangan prima, buat daftar yang baru di mana setiap elemen dari daftar saat ini, termasuk yang pertama, dikali oleh nomor pertama yang ditambahkan.
• Kurangi list baru dari list saat ini. simpan kedalam list hasil untuk angka yang di list saat ini dan tidak ada di list baru. Buat list hasil agar digabungkan ke list saat ini, kecualikan elemen pertama yang didalam list saat ini.
• Ulangi Langkah 2, 3, dan 4 untuk list saat ini sampai list saat ini kosong.

Berapa banyak pengurangan didalam list untuk mendapatkan 10 bilangan prima pertama?

Pembahasan

Kita perlu untuk melihat pola yang konsisten. Pertama setelah pengurangan kita mendapatkan sebuah bilangan prima – 2. Kemudian, saat permulaan, muncul bilangan prima kedua – 3, dan kemudian kita melakukan pengurangan lagi. Saat kali ketiga, setelah pengurangan, kita dapat bilangan prima ketiga – 5, keempat – keempat bilangan prima -7, dan seterusnya. Jadi, Ketika kita ingin mendapatkan 10 bilangan prima pertama, kita perlu melakukan pengurangan lagi list nya sebanyak 10x

---

Di bidang Ilmu Komputer, binary search atau yang lebih dikenal dengan half-interval search, membagi dan menaklukkan, atau binary chop adalah search algorithm yang mencari posisi value target dengan mensortit array.  Binary search membandingkan nilai target dengan elemen tengah dari array; jika mereka tidak sama, dihilangkan dan pencarian berlanjut pada setengah sisanya sampai berhasil. Jika pencarian berakhir dengan setengah sisanya kosong, artinya targetnya tidak ada dalam larik. Contoh terkenal memiliki sembilan koin yang beratnya identik, kecuali satu, yang dalam contoh ini lebih ringan dari yang lain – palsu. Perbedaannya hanya per terlihat dengan menimbangnya pada skala keseimbangan – tetapi hanya koin itu sendiri yang bisa ditimbang.

Apakah mungkin untuk mengisolasi koin palsu hanya dengan dua penimbangan? 

Pembahasan

Kita tahu bahwa koin palsu lebih banyak daripada yang asli, jadi dimungkinkan untuk mendefinisikan koin palsu.

dengan menimbang dua kali. Cara membuatnya bisa dilihat pada gambar di bawah ini.

---

Berang-berang ingin berenang di setiap kanal tepat satu kali, dimulai dan berakhir di kanalnya (pondok A). (Ketika jalur Euler dimulai dan berakhir pada titik yang sama, itu disebut sirkuit Euler.) Berang-berang ini menggunakan algoritma Fleur yang ide utamanya adalah: 

“pada setiap Langkah, jika dia bisa, dia memilih ke kanal berikutnya untuk tidak menjadi “sebuah jembatan” untuk bagian yang belum dijelajahi (sebuah jembatan didefinisikan sebagai vortex yang menghapus dan membagi grafik menjadi dua bagian yang tidak tersambung – bakar jembatan di belakang anda dan anda tidak bisa Kembali ke tempat anda sebelumnya). Jika tidak ada semacam kanal “non-bridge”, maka ambil kanal tersebut  

Langkah 1 : A ke B 

Langkah 2 : B ke C

Langkah 3 : C ke E (C ke D hanyalah menjembatani saja)

Langkah 4 : E ke F

Langkah 5 : pilih yang mana kanal F ke C, F ke G atau F to I?

Berapa banyak Langkah lagi untuk menyelesaikan sirkuit Eulerian nya?

Pembahasan

FC di Langkah ke 5 hanya menjadi jembatan, setelah melewati itu, kita tidak bisa Kembali lagi ke paragraf yang benar. Channels FG dan FI adalah sama, dan kita bisa pilih salah satu dari nya. Dan Eulerian circuit bisa diselesaikan dalam 11 langkah.

---

Seekor berang-berang ingin membikin jaringan pipa sehingga air dari sumber utama A bisa ke setiap shower (A, B, C, D, E, F, G, H, I). dia juga mau melakukan se hemat mungkin. Setiap angka di pipa mengindikasikan setiap harga untuk instalasi pipa tersebut.

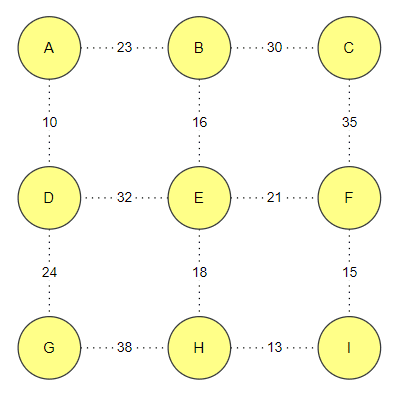
Berang-berang mengetahui Kruskal Algorithm 

• Cari titik dengan ongkos yang paling murah (jika titik tersebut lebih dari 1, pilih secara acak). Tandai.
• Cari titik selanjutnya dengan biaya yang lebih murahm, titik yang tidak ditandai. Jika titik tersebut sudah ditandai dengan sebelumnya, abaikan itu dan buang dari seleksi selanjutnya. Jika tidak, maka tandai itu 
• Ulangi Langkah kedua sampai semua titik terkoneksi

Kemudian ia mengaplikasikan algoritma tersebut: 

1. Tandai AD
2. HI
3. FI
4. BE
5. EH
6. EF. Circuit. Hapus ED
7. …

Lanjutkan dan cari jaringan dengan biaya termurah untuk instalasi pipa tersebut. Seperti apa nanti jaringan nya?

Pembahasan

Di Langkah sebelumnya yang dijelaskan, kita membangun pipa AB, DG, dan BC. Semua pipa akan membuat sirkuit, jadi kita tidak perlu membangun nya lagi

Dan pembuatan channel akan memakan biaya: 

10 + 24 + 23 + 30 + 16 + 18 + 13 + 15 = 149

---

1. Sekarang, 3 ekor berang-berang ingin membangun sebuah bendungan dan perlu melakukan 7 tugas: A(7), B(5), C(8), D(13), E(7), G(2). Angka yang didalam kurung mengindikasikan jumlah jam kerja. Sebagian tugas harus diselesaikan sebelum yang lain bisa dimulai. Garis yang dahulu harus dikerjakan ditandai dengan arah panah. Kita tambahkan start dan finish, agar memudahkan kita untuk memvisualisasi dan mengarahkan graph.

Berang-berang menggunakan Decreasing Time Algorithm (DTA) : dari semua tugas yang tersedia sekarang, mereka harus memilih yang durasi lama terlebih dahulu.

Bikinlah time-table. Beberapa lama waktu yang mereka butuhkan untuk menyelesaikan bendungan tersebut?

Pembahasan

Decreasing time list akan seperti ini: D(13), C(8), A(7), E(7), B(5), G(2), F(1). Maka dari itu, kita tidak bisa memulai task D(13) sampai task A dan B selesai. Kita harus membuat schedule menggunakan Decreasing Time Algorithm 

Dengan menggunakan decreasing time algorithm, 3 beruang akan membangun bendungan dalam 21 jam

---

1. Seekor berang-berang ingin menghitung jumlah jalur yang pendek dari mulai ke setiap intersection didalam kisi-kisi persegi. Nilainya harus bisa dihitung baris kali baris bawah dan bergerak dari kiri ke kanan sepanjang setiap baris. Bagaimanapun, pasti ada jalur yang patah. Berang-berang ingin menggunakan Dynamic Programming method yang sebagaimana menyelesaikan setiap sub masalah dalam hanya sekali jalan dan merekam hasilnya di meja dari solusi hingga masalah yang bisa diperoleh.

Bantulah berang-berang untuk mengisi lingkaran yang kosong

Pembahasan

Menghitung jalur adalah bentuk aplikasi dari dynamic programming. Pendekatan ini bertujuan mencari berapa jalur terdekat dari start ke setiap intersection didalam kisi-kisi tersebut. Kisi-kisi yang pecah tidak akan dihitung, apabila didalam intersection ada yang terkoneksi antara neighbour kiri dan neighbour atas, maka akan dihitung berdasarkan jumlah neighbouring; jika ada interseksi hanya ada satu neighbours, maka akan dihitung berdasarkan jumlah neighbours tersebut

---

1. Tiga serangkai berang-berang ini adalah akrobatik yang lihai. Mereka melakukan sebuah performa yang special, berang yang besar ada di paling bawah, diatas nya ada yang beratnya sedang dan yang paling atas adalah berang-berang yang paling kecil. Mereka berdiri diantara tiga tunggul dan mereka harus lompat ke tunggul yang lain dengan aturan dibawah ini : 

• Lompat 1 per 1
• Harus berdiri diatas tunggul itu atau satu diatas yang lain;
• Beruang yang besar tidak bisa berdiri diatas yang paling kecil

Sedikit memakan waktu untuk berang berang melompat ke tunggul yang lain. Ini adalah cara untuk bagaimana berang-berang tersebut bisa melompat, berikut penampakannya:

Setelah kita lihat, berang-berang membutuhkan waktu 7 menit untuk lompat diantara tunggul tersebut

Berapa menit untuk melompat dari satu tunggul ke tunggul yang lain, dengan peraturan yang sama, untuk empat berang-berang yang akrobat?

Pembahasan

Tandai berang-berang yang besar dengan D, yang sedang dengan V, yang kecil dengan M. kemudian kita bisa menulis semua lompatan yang berang-berang buat. Bagaimana pun, kitab isa mencari solusi yang mana hanya membutuhkan sedikit penulisan. Didalam itu, lompatan yang akan dilakukan 4 berang-berang tersebut sedikit sama dengan 3 berang-berang, – hanya saja tugasnya lebih kecil satu unit. Katakanlah kita tahu bagaimana 3 berang-berang melompat. Maka hanya yang terakhir dan berang-berang terbesar yang tersisa. Dia akan mengambil 1 menit untuk melompat. Ketika berang-berang terbesar melompat pada tunggul yang kosong, maka ketiga berang-berang dapat melompat di atasnya – jadi kita tahu itu akan memakan waktu 7 menit.

Oleh karena itu semua berang-berang akan bertahan 7 + 1 + 7 = 15 menit.